Meshes for spectral functions

The spectral function $A(\omega)$ is defined on the real frequency axis. The frequency range for $\omega$ is restricted in $[\omega_{\text{min}}, \omega_{\text{max}}]$, where $N_{\omega}$ represents the number of mesh points, $\omega_{\text{min}}$ and $\omega_{\text{max}}$ denote the left and right boundaries of the mesh, respectively. Currently, the ACTest toolkit supports four types of meshes: linear, tangent, Lorentzian, and half-Lorentzian meshes. The latter three meshes are non-linear, with the highest grid density near $\omega = 0$. As its name suggests, the half-Lorentzian mesh is only suitable for cases where $\omega \ge 0$. Figure 1 illustrates typical examples of the four meshes.

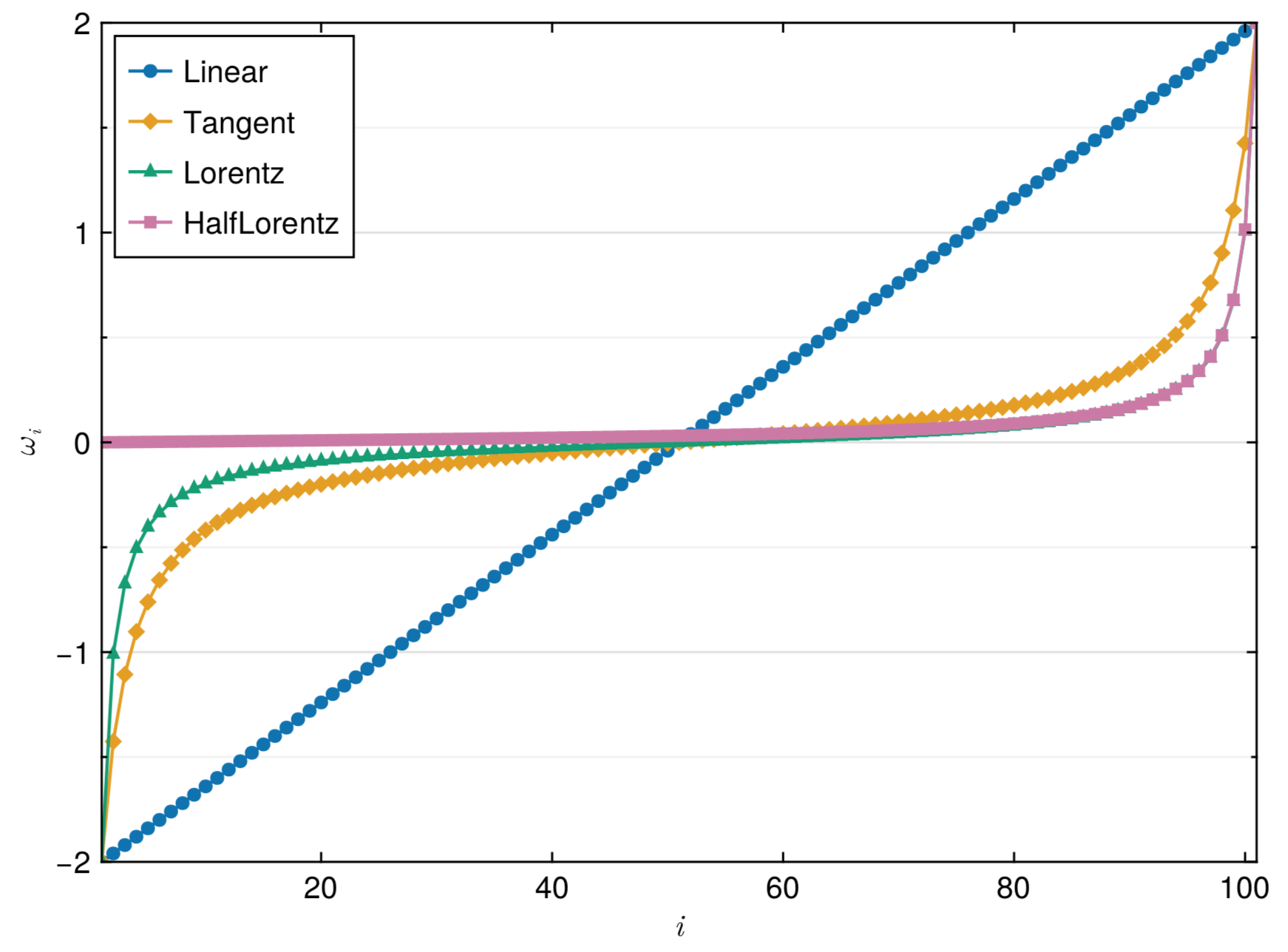
Figure 1 | The four frequency meshes supported in ACTest: linear, tangent, Lorentzian, and half-Lorentzian meshes. The parameters for these meshes are $\omega_{\text{max}} = -\omega_{\text{min}} = 2.0$ and $N_{\omega} = 101$.